Erklärungen: Texte von ChatGPT
Sortieralgorithmen:
Sortieralgorithmen sind Algorithmen, die eine Liste von Elementen in einer bestimmten Reihenfolge anordnen. Es gibt viele verschiedene Sortieralgorithmen, die sich in ihrer Effizienz, ihrem Speicherbedarf und ihrer Stabilität unterscheiden. Einige der bekanntesten Sortieralgorithmen sind hier aufgeführt.
Details:
- Zeitkomplexität: Die Zeitkomplexität eines Algorithmus gibt an, wie sich die Laufzeit des Algorithmus in Abhängigkeit von der Größe der Eingabe verhält. Sie wird oft in der sogenannten Big-O-Notation angegeben, die das Wachstum des Algorithmus in Bezug auf die Anzahl der Elemente in der Eingabe beschreibt.
- O steht dabei für "Ordnung von" und gibt an, wie schnell der Algorithmus im schlimmsten Fall ausgeführt wird. Zum Beispiel bedeutet O(n^2), dass der Algorithmus quadratisch wächst, was bedeutet, dass die Laufzeit quadratisch mit der Anzahl der Elemente in der Eingabe zunimmt.
- n steht dabei für die Anzahl der Elemente in der Eingabe.
- k steht für die Anzahl der möglichen Werte, die die Elemente annehmen können.
- Autor: Der Autor des Algorithmus, falls bekannt.
- Jahr: Das Jahr, in dem der Algorithmus entwickelt wurde.
Benutzte Farben:
- ■ Lesen: Ein Lesezugriff auf ein Element der Liste.
- ■ Tauschen: Ein Tauschvorgang zwischen zwei Elementen der Liste.
- ■ Schreiben: Ein Schreibzugriff auf ein Element der Liste.
- ■ Fertig: Ein Element ist an der richtigen Position.
Benutzte Methoden der Math Klasse:
- Math.random(): Gibt eine Pseudozufallszahl zwischen 0 und 1 zurück.
- Math.floor(): Rundet eine Zahl auf die nächstkleinere Ganzzahl ab.
- Math.max(): Gibt die größte Zahl einer Liste von Zahlen zurück.
- Math.min(): Gibt die kleinste Zahl einer Liste von Zahlen zurück.
Eigene Methoden:
- swap(i, j): Vertauscht die Balken an den Positionen i und j.
Shuffle
Der Shuffle-Algorithmus ist ein einfacher Algorithmus, der die Elemente einer Liste zufällig neu anordnet. Er wird oft verwendet, um eine Liste vorzubereiten, bevor ein Sortieralgorithmus angewendet wird, um sicherzustellen, dass der Algorithmus nicht von der ursprünglichen Reihenfolge der Elemente beeinflusst wird.
Details:
- Zeitkomplexität: O(n)
Psuedocode:
for i from 0 to n-1:
randomIndex = random number between i and n-1
swap elements at index i and randomIndexJavaScript:
for(let i = 0; i < n; i++){
let randomIndex = Math.floor(Math.random() * n);
swap(i, randomIndex);
}Bogo Sort:
Der Bogo Sort, auch bekannt als Permutation Sort oder Monkey Sort, ist ein äußerst ineffizienter Sortieralgorithmus, der die Elemente einer Liste zufällig neu anordnet und prüft, ob sie sortiert sind. Dieser Prozess wird so lange wiederholt, bis die Liste sortiert ist. Aufgrund seiner zufälligen Natur und der Tatsache, dass er im schlimmsten Fall eine nahezu unendliche Anzahl von Permutationen durchlaufen muss, hat der Bogo Sort keinen praktischen Nutzen und wird meist als Lehrbeispiel verwendet, um zu zeigen, wie ineffizient ein Algorithmus sein kann.
Details:
- Zeitkomplexität im besten Fall: O(n)
- Zeitkomplexität im schlechtesten Fall: Unendlich
Psuedocode:
while(!isSorted()){
shuffle();
}
JavaScript:
while(!isSorted()){
shuffle();
}
Bubble Sort:
Der Bubble Sort ist ein einfacher, aber ineffizienter Sortieralgorithmus, der wiederholt benachbarte Elemente vergleicht und vertauscht, wenn sie in der falschen Reihenfolge sind. Dies wird so lange wiederholt, bis keine Vertauschungen mehr nötig sind, was bedeutet, dass die Liste sortiert ist. Der Name "Bubble Sort" kommt daher, dass die kleineren Elemente wie Blasen an die Oberfläche steigen.
Details:
- Zeitkomplexität: O(n^2)
- Autor: Ivan Sutherland und Bob Floyd
- Jahr: 1962
Psuedocode:
for i ← 0 to A[].Len-1 do
for j ← 1 to A[].Len-1 do
if A[j-1] > A[j] Then
lastJ ← A[j-1]
A[j-1] ← A[j]
A[j] ← lastJ
End if
End for
End forJavaScript:
for(let i = 0; i < n; i++){
for(let j = 1; j < n; j++){
if(array[j-1] > array[j]){
swap(j-1, j);
}
}
}Selection Sort:
Der Selection Sort ist ein Sortieralgorithmus, der die Liste in zwei Teile teilt: den sortierten und den unsortierten Teil. Der Algorithmus wiederholt den Prozess, das kleinste Element aus dem unsortierten Teil zu finden und es an die richtige Position im sortierten Teil zu verschieben. Dieser Prozess wird fortgesetzt, bis die gesamte Liste sortiert ist.
Details:
- Zeitkomplexität: O(n^2)
- Autor: Edward H. Friend
- Jahr: 1956
Pseudocode:
for i from 0 to n-1:
min = i
for j from i+1 to n:
if array[j] < array[min]:
min = j
if min != i:
swap elements at index i and minJavaScript:
for(let i = 0; i < n; i++){
let min = i;
for(let j = i+1; j < n; j++){
if(array[j] < array[min]){
min = j;
}
}
if(min !== i){
swap(i, min);
}
}Insertion Sort:
Der Insertion Sort ist ein einfacher Sortieralgorithmus, der die Elemente der Liste nacheinander durchgeht und jedes Element in die richtige Position in der bereits sortierten Teilliste einfügt. Dies wird erreicht, indem man die Elemente mit den vorhergehenden Elementen vergleicht und sie so lange verschiebt, bis das aktuelle Element an der richtigen Stelle steht.
Details:
- Zeitkomplexität: O(n^2)
- Autor: John von Neumann
- Jahr: 1946
Psuedocode:
for i from 1 to n-1:
key = array[i]
j = i - 1
while j >= 0 and array[j] > key:
array[j+1] = array[j]
j = j - 1
array[j+1] = keyJavaScript:
for(let i = 1; i < n; i++){
let key = array[i];
let j = i - 1;
while(j >= 0 && array[j] > key){
array[j+1] = array[j];
j = j - 1;
}
array[j+1] = key;
}Merge Sort:
Der Merge Sort ist ein effizienter, vergleichsbasierter Sortieralgorithmus, der auf dem Prinzip "Teile und herrsche" basiert. Er teilt die Liste wiederholt in zwei Hälften, sortiert jede Hälfte rekursiv und führt die beiden sortierten Hälften zusammen. Der Algorithmus zeichnet sich durch seine stabile Sortierung und seine Zeitkomplexität von O(n log n) aus.
Details:
- Zeitkomplexität: O(n log n)
- Autor: John von Neumann
- Jahr: 1945
JavaScript:
function mergeSort(array){
if(array.length <= 1){
return array;
}
let middle = Math.floor(array.length / 2);
let left = array.slice(0, middle);
let right = array.slice(middle);
return merge(mergeSort(left), mergeSort(right));
}
function merge(left, right){
let result = [];
let i = 0;
let j = 0;
while(i < left.length && j < right.length){
if(left[i] < right[j]){
result.push(left[i]);
i++;
}else{
result.push(right[j]);
j++;
}
}
return result.concat(left.slice(i)).concat(right.slice(j));
}Quick Sort:
Der Quick Sort ist ein effizienter, vergleichsbasierter Sortieralgorithmus, der ebenfalls auf dem Prinzip "Teile und herrsche" basiert. Er wählt ein "Pivot"-Element aus der Liste aus, teilt die Liste in zwei Unterlisten – eine mit Elementen, die kleiner sind als das Pivot, und eine mit Elementen, die größer sind – und sortiert diese Unterlisten rekursiv. Der Algorithmus ist bekannt für seine gute durchschnittliche Leistung und seine Zeitkomplexität von O(n log n).
Details:
- Zeitkomplexität: O(n log n)
- Autor: Tony Hoare
- Jahr: 1960
JavaScript:
function quickSort(array, low, high){
if(low < high){
let pi = partition(array, low, high);
quickSort(array, low, pi - 1);
quickSort(array, pi + 1, high);
}
}
function partition(array, low, high){
let pivot = array[high];
let i = low - 1;
for(let j = low; j < high; j++){
if(array[j] < pivot){
i++;
swap(array, i, j);
}
}
swap(array, i + 1, high);
return i + 1;
}Heap Sort:
Der Heap Sort ist ein effizienter, vergleichsbasierter Sortieralgorithmus, der die Elemente der Liste in einen Heap umwandelt und sie dann sortiert, indem er wiederholt das größte Element entfernt und an das Ende der sortierten Liste stellt.
Details:
- Zeitkomplexität: O(n log n)
- Autor: J. W. J. Williams
- Jahr: 1964
JavaScript:
function heapSort(array){
let n = array.length;
for(let i = Math.floor(n / 2) - 1; i >= 0; i--){
heapify(array, n, i);
}
for(let i = n - 1; i >= 0; i--){
swap(array, 0, i);
heapify(array, i, 0);
}
}
function heapify(array, n, i){
let largest = i;
let l = 2 * i + 1;
let r = 2 * i + 2;
if(l < n && array[l] > array[largest]){
largest = l;
}
if(r < n && array[r] > array[largest]){
largest = r;
}
if(largest !== i){
swap(array, i, largest);
heapify(array, n, largest);
}
}Radix Sort:
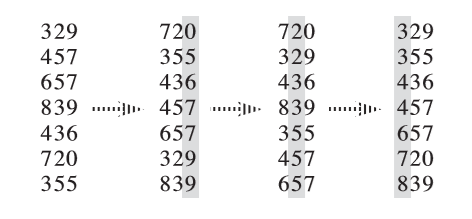
Der Radix Sort ist ein nicht vergleichsbasierter Sortieralgorithmus, der die Elemente nach ihren Ziffern sortiert, beginnend mit der niederwertigsten Ziffer. Er verwendet einen stabilen Hilfssortieralgorithmus wie Counting Sort, um die Elemente basierend auf ihren Ziffern zu sortieren.
Details:
- Zeitkomplexität: O(nk)
- Autor: Herman Hollerith
- Jahr: 1887
JavaScript:
function countingSort(array, exp){
let output = new Array(array.length);
let count = new Array(10).fill(0);
for(let i = 0; i < array.length; i++){
count[Math.floor(array[i] / exp) % 10]++;
}
for(let i = 1; i < 10; i++){
count[i] += count[i - 1];
}
for(let i = array.length - 1; i >= 0; i--){
output[count[Math.floor(array[i] / exp) % 10] - 1] = array[i];
count[Math.floor(array[i] / exp) % 10]--;
}
for(let i = 0; i < array.length; i++){
array[i] = output[i];
}
}
function radixSort(array){
let max = Math.max(...array);
for(let exp = 1; Math.floor(max / exp) > 0; exp *= 10){
countingSort(array, exp);
}
} Shell Sort:
Der Shell Sort ist ein effizienter, vergleichsbasierter Sortieralgorithmus, der die Liste in mehrere Teile teilt und diese Teile separat sortiert. Er verwendet eine sich verringernde Sequenz von Intervallen, um die Liste zu sortieren, was dazu führt, dass die Liste schneller konvergiert.
Details:
- Zeitkomplexität: O(n log n)
- Autor: Donald Shell
- Jahr: 1959
JavaScript:
function shellSort(array){
let n = array.length;
for(let gap = Math.floor(n / 2); gap > 0; gap = Math.floor(gap / 2)){
for(let i = gap; i < n; i++){
let temp = array[i];
let j;
for(j = i; j >= gap && array[j - gap] > temp; j -= gap){
array[j] = array[j - gap];
}
array[j] = temp;
}
}
}Counting Sort:
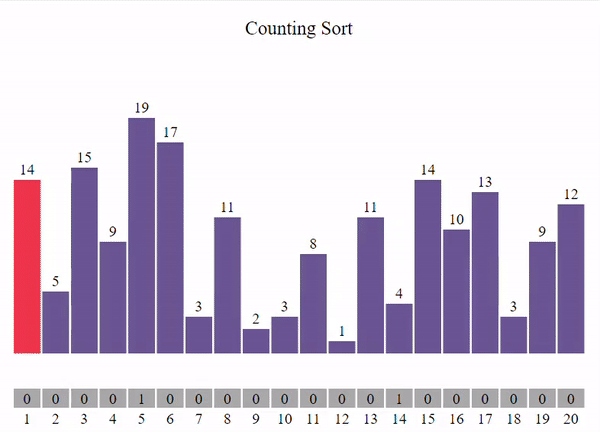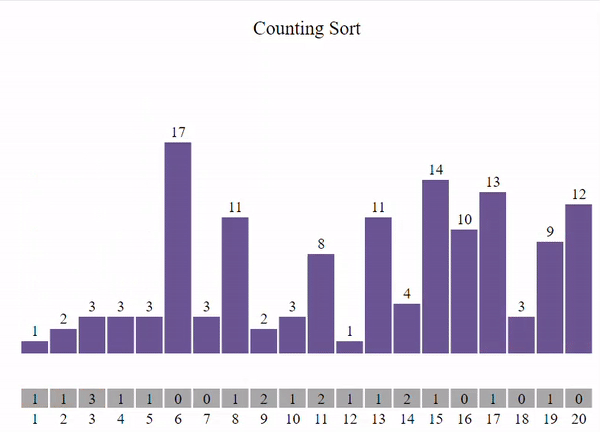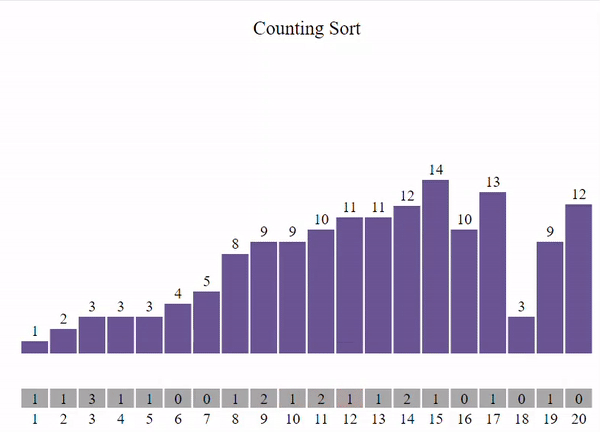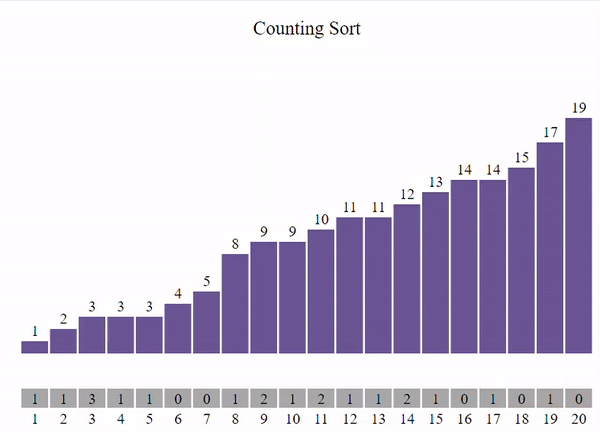
Der Counting Sort ist ein nicht vergleichsbasierter Sortieralgorithmus, der die Elemente der Liste nach ihrer Häufigkeit sortiert. Er verwendet ein Zähl-Array, um die Häufigkeit jedes Elements zu zählen und diese Zählungen dann zu verwenden, um die Elemente in die richtige Reihenfolge zu bringen.
Details:
- Zeitkomplexität: O(n + k)
- Jahr: Unbekannt
JavaScript:
function countingSort(array){
let n = array.length;
let max = Math.max(...array);
let min = Math.min(...array);
let range = max - min + 1;
let count = new Array(range).fill(0);
let output = new Array(n).fill(0);
for(let i = 0; i < n; i++){
count[array[i] - min]++;
}
for(let i = 1; i < count.length; i++){
count[i] += count[i - 1];
}
for(let i = n - 1; i >= 0; i--){
output[count[array[i] - min] - 1] = array[i];
count[array[i] - min]--;
}
for(let i = 0; i < n; i++){
array[i] = output[i];
}
} Cocktail Sort:
Der Cocktail Sort, auch bekannt als Bidirectional Bubble Sort, ist eine Variante des Bubble Sort, die die Elemente in beide Richtungen sortiert. Der Algorithmus geht wiederholt von links nach rechts und dann von rechts nach links durch die Liste und vertauscht benachbarte Elemente, die in der falschen Reihenfolge sind.
Details:
- Zeitkomplexität: O(n^2)
- Autor: Edward H. Friend
- Jahr: 1956
JavaScript:
function cocktailSort(array){
let n = array.length;
let swapped = true;
let start = 0;
let end = n - 1;
while(swapped){
swapped = false;
for(let i = start; i < end; i++){
if(array[i] > array[i + 1]){
swap(array, i, i + 1);
swapped = true;
}
}
if(!swapped) break;
swapped = false;
end--;
for(let i = end - 1; i >= start; i--){
if(array[i] > array[i + 1]){
swap(array, i, i + 1);
swapped = true;
}
}
start++;
}
} Comb Sort:
Der Comb Sort ist eine Variante des Bubble Sort, die versucht, dessen Hauptproblem – kleine benachbarte Vertauschungen – zu beheben, indem sie größere Abstände zwischen den verglichenen Elementen verwendet. Der Algorithmus beginnt mit einem großen Abstand und verringert diesen schrittweise, bis er auf 1 reduziert ist.
Details:
- Zeitkomplexität: O(n^2)
- Autoren: Wlodzimierz Dobosiewicz und Stephen Lacey, Richard Box
- Jahr: 1980 bzw. 1981
JavaScript:
function combSort(array){
let n = array.length;
let gap = n;
let swapped = true;
while(gap !== 1 || swapped){
gap = Math.floor(gap / 1.3);
if(gap < 1) gap = 1;
swapped = false;
for(let i = 0; i < n - gap; i++){
if(array[i] > array[i + gap]){
swap(array, i, i + gap);
swapped = true;
}
}
}
} Gnome Sort:
Der Gnome Sort, auch bekannt als Stupid Sort, ist ein einfacher Sortieralgorithmus, der die Elemente der Liste nacheinander durchgeht und sie an die richtige Stelle verschiebt. Der Algorithmus funktioniert ähnlich wie der Insertion Sort, indem er Elemente wiederholt mit den vorhergehenden vergleicht und sie vertauscht, wenn sie in der falschen Reihenfolge sind.
Details:
- Zeitkomplexität: O(n^2)
- Autor: Hamid Sarbazi-Azad
- Jahr: 2000
JavaScript:
function gnomeSort(array){
let index = 0;
while(index < array.length){
if(index === 0 || array[index] >= array[index - 1]){
index++;
}else{
swap(array, index, index - 1);
index--;
}
}
} Odd-Even Sort:
Der Odd-Even Sort ist ein einfacher Sortieralgorithmus, der die Elemente der Liste abwechselnd sortiert. Der Algorithmus vergleicht jedes Element mit seinem nachfolgenden Element und vertauscht sie, wenn sie in der falschen Reihenfolge sind. Dieser Prozess wird wiederholt, bis die Liste sortiert ist.
Details:
- Zeitkomplexität: O(n^2)
- Autor: Unbekannt
- Jahr: Unbekannt
JavaScript:
function oddEvenSort(array){
let sorted = false;
while(!sorted){
sorted = true;
for(let i = 1; i < array.length - 1; i += 2){
if(array[i] > array[i + 1]){
swap(array, i, i + 1);
sorted = false;
}
}
for(let i = 0; i < array.length - 1; i += 2){
if(array[i] > array[i + 1]){
swap(array, i, i + 1);
sorted = false;
}
}
}
} Cycle Sort:
Der Cycle Sort ist ein effizienter Sortieralgorithmus, der die Elemente der Liste an ihre richtige Position verschiebt, indem er die Zyklen in der Liste erkennt. Der Algorithmus ist bekannt für seine minimale Anzahl von Schreibzugriffen und seine Zeitkomplexität von O(n^2).
Details:
- Zeitkomplexität: O(n^2)
- Autor: Harold N. Gabow
- Jahr: 1975
JavaScript:
function cycleSort(array){
let n = array.length;
for(let cycleStart = 0; cycleStart < n - 1; cycleStart++){
let item = array[cycleStart];
let pos = cycleStart;
for(let i = cycleStart + 1; i < n; i++){
if(array[i] < item){
pos++;
}
}
if(pos === cycleStart){
continue;
}
while(item === array[pos]){
pos++;
}
let temp = array[pos];
array[pos] = item;
item = temp;
while(pos !== cycleStart){
pos = cycleStart;
for(let i = cycleStart + 1; i < n; i++){
if(array[i] < item){
pos++;
}
}
while(item === array[pos]){
pos++;
}
temp = array[pos];
array[pos] = item;
item = temp;
}
}
} Stooge Sort:
Der Stooge Sort ist ein rekursiver Sortieralgorithmus, der die Elemente der Liste in drei Teile teilt und die ersten zwei Drittel rekursiv sortiert, gefolgt von den letzten zwei Dritteln und schließlich den ersten zwei Dritteln erneut. Der Algorithmus ist bekannt für seine schlechte Leistung und seine Zeitkomplexität von O(n^2.7).
Details:
- Zeitkomplexität: O(n^2.7)
- Autor: Homer Reith
- Jahr: 1975
JavaScript:
function stoogeSort(array, l, h){
if(l >= h){
return;
}
if(array[l] > array[h]){
swap(array, l, h);
}
if(h - l + 1 > 2){
let t = Math.floor((h - l + 1) / 3);
stoogeSort(array, l, h - t);
stoogeSort(array, l + t, h);
stoogeSort(array, l, h - t);
}
} Pancake Sort:
Der Pancake Sort ist ein Sortieralgorithmus, der die Elemente der Liste durch Umkehren sortiert. Der Algorithmus wählt das größte Element aus und wendet eine Reihe von Umkehrungen an, um es an die richtige Position zu bringen. Der Pancake Sort ist bekannt für seine minimale Anzahl von Schreibzugriffen und seine Zeitkomplexität von O(n^2).
Details:
- Zeitkomplexität: O(n^2)
- Autor: Jacob E. Goodman, William H. Gates, Christos H. Papadimitriou
- Jahr: 1979
JavaScript:
function pancakeSort(array){
let n = array.length;
for(let i = n; i > 1; i--){
let maxIndex = findMaxIndex(array, i);
if(maxIndex !== i - 1){
flip(array, maxIndex);
flip(array, i - 1);
}
}
}
function findMaxIndex(array, n){
let maxIndex = 0;
for(let i = 0; i < n; i++){
if(array[i] > array[maxIndex]){
maxIndex = i;
}
}
return maxIndex;
}
function flip(array, i){
let start = 0;
while(start < i){
swap(array, start, i);
start++;
i--;
}
}